Science & Fun - Jonathan Graehl

A lower level (Scala) solution to this puzzle:

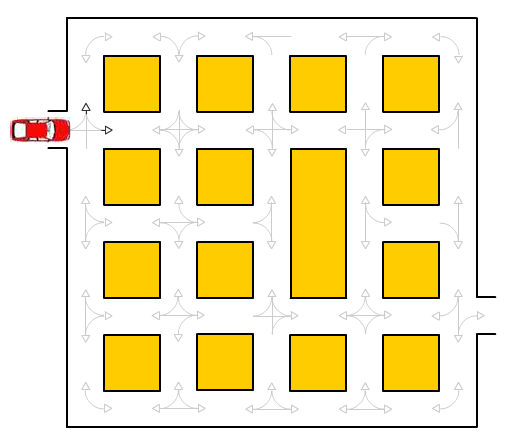
There’s a path from the car to the exit on the right following the lines at corners, and emerging only at arrowheads. This is just a directed graph.  The two directions on a street segment are independent nodes.  I stole from Daniel Sobral the text representation of the graph, and implemented breadth first (shortest path) search just like he did.  The difference is that I explicitly represent the directed graph, and I do so in typical programming contest style.  He has a nice ASCII art printout; I just used simple debug prints to verify that I built the graph right.

It bothers me that in JVM languages, wrapping a primitive in a type requires boxing (no matter how awesome just-in-time compilation is, there’s still memory overhead).  So I end up using a lot of bare primitives and arrays of primitives, probably to my detriment.  Clearly it’s not relevant for this problem (which even a human can solve), but it might eventually compel me to use C++ again (where things are miserable, but at least there’s no abstraction penalty).  I believe .NET allows C-like structures of unboxed primitives, but I’m not satisfied that F# is as pleasant or efficient as Scala (even using my primitive-happy style).

Obviously, most of the code is about translating the text graph description to the directed adjacency list.  It’s about half the lines of his version, but I won’t claim it’s easier to understand.

final case class Roadmap(rows: Int,cols: Int) {
  type Onto=Array[Int] // adjacency list
  type Roads=Array[Onto] // vertices (unidirectional road segments)
  val RC=rows*cols
  val ndir=4
  val goal=RC*ndir
  val DRC=RC*ndir
  val roads=new Roads(DRC) // one dimensional array allows for simpler adjacencies at the cost of uglier addressing
  /* separate road segment for each direction right left down up (0 1 2 3)
   so that (row,col) is the location of the upper/left corner of that segment (be consistent!)
   */
  def index(rldu: Int,row: Int, col: Int) = RC*rldu+row*cols+col
  def coord(i: Int) = { val rldu=i/RC;val r=i%RC;(rldu,r/cols,r%cols) }
  val R=0
  val L=1
  val D=2
  val U=3
  val NONE=4
  def c2dir(a: Char) = a match {
    case ‘R’ => R
    case ‘L’ => L
    case ‘D’ => D
    case ‘U’ => U
    case _ => NONE
  }
  def dir2c(d: Int) = “RLDUN”(d)
  def coordname(t: (Int,Int,Int))=t match {case (rldu,row,col) => “%c%d%d”.format(dir2c(rldu),row,col)}
  def i2s(i: Int)=coordname(coord(i))
  /* set the transitions that meet in the intersection on row r, col c.
     exits(dir) if there’s an arrowhead; undir is a list of pairs of linked dirs */
  def setCorner(r: Int, c: Int, exits: Array[Boolean], undirs: Array[(Int,Int)], goaldir: Int) {
    // remember, r,c gives the upper/left part of road
    val froms=Array(index(L,r,c),index(R,r,c-1),index(U,r,c),index(D,r-1,c))
    // to approach from the right, you head left.  froms and tos are identical except opposite directions
    val tos=  Array(index(R,r,c),index(L,r,c-1),index(D,r,c),index(U,r-1,c))
    val ways= Array.fill(ndir)(new collection.mutable.ArrayBuffer[Int](ndir))
    def checkdir(from: Int,to: Int) {
      if (goaldir==to) ways(from)+=goal
      else if (exits(to)) ways(from)+=tos(to)
    }
    for ((from,to)       checkdir(from,to)
      checkdir(to,from)
    }
    for ((f,w)       if (w.size>0) roads(f)=w.toArray
      // since we didn’t pad the border, we’ve considered indices that are off the array.
      // user input must not ask us to move from somewhere off the array
      // a padded border would prevent this, and allow a single start and goal state
    }
  }
  def s2dirs(s: String) = (c2dir(s(0)),c2dir(s(1)))
  def readCorner(r: Int, c: Int, desc: String) {
    val a=desc.trim split “:”
    val exits=new Array[Boolean](ndir)
    var lastdir=NONE
    var goaldir=lastdir
    for ( c       if (c==’!’) goaldir=lastdir
      else {
        val d=c2dir(c)
        if (d!=NONE) {
          exits(d)=true
          lastdir=d
        }
      }
    }
    setCorner(r,c,exits,a(1).trim split ” ” map s2dirs toArray,goaldir)
  }
  def read(s: String) = {
    var r=0
    for ((line,row)=0) zipWithIndex) {
      for ((s,col)         readCorner(row,col,s)
      }
    }
  }
  def path2goal(starts: Int*) = {
    type Path=List[Int]
    val q=new collection.mutable.Queue[Path]
    val seen=new Array[Boolean](DRC)
    starts foreach (seen(_)=true)
    val s=starts map (x=>List(x))
    q.enqueue(s: _*)
    var p=q.head
    while (p.head != goal) {
      val h=p.head
      seen(h)=true
      val n=roads(h) map (_::p)
      q enqueue (n: _*)
      p=q dequeue
    }
    p
  }
  def prettypath(p: List[Int]) = p reverseMap i2s
}

object car {
/* from http://dcsobral.blogspot.com/2009/09/puzzle.html */
  val graphString = “”“|
                       |DR: DR, RLD: RD LD, L: DL LR, LR: DR LR, DL: DL
                       |UR: LU RU DU LR, LRD: LR UD LU RU LD RD, UDLR: UD LR UR LD, UDLR: UD LR RD, UL: UD UL
                       |UDR: UD RU RD, UDLR: LR LD DR RU, UD: UD UL DL, UDR: UD UR, UD: UD LD
                       |UDR: UD RU RD, UDLR: UR UL LR RD, UR: UD LR LU RU DR, ULR: LR UR UL DR DL, UDLR!: UD UL DR
                       |UR: UR, ULR: UL UR LR, ULR: UL UR RL, ULR: UL UR RL, UL: UL
                       |”“”.stripMargin
  def main(args: Array[String]) {
    val r=Roadmap(5,5)
    r.read(graphString)
    println(r.prettypath(r.path2goal(r.index(r.R,1,0),r.index(r.U,0,0))))
  }
}

The format is explained on Daniel’s blog, but I found it odd enough that I’ll mention that it’s a matrix of intersections with EXITS: UNDIRECTED_ADJACENCIES.  EXITS is the list of directions that have a departing arrowhead.  The adjacencies are undirected to save typing (UR means both UR and RU).  I added a ! following the arrowhead if it leads to the goal, since I didn’t want to hard code the exit location.

Because I didn’t create any node for the car’s starting location, I just started the search from both the initial turns available.

(SPOILER: R10, R11, D12, D22, R32, U23, U13, U03, R03, D04, L13, D13, R23, D24, D34, L43, L42, L41, L40, U30, U20, R20, D21, L30, D30, R40, R41, R42, R43, U34, where 32 means the road segment with its upper left at row 3 and column 2)

https://gist.github.com/181632