Science & Fun - Jonathan Graehl

Fast Translation Rule Matching for Syntax-based Statistical Machine Translation
in EMNLP09 (Zhang et. al) gives a practical method for top-down enumerating tree pattern matches against the root of a forest (compact regular set of trees).  This problem arises in MT when you first context-free-parse your source material, and then transform its syntax tree into another language - since parsers aren’t perfect, you translate all the likely parses rather than just the most likely, and pick the most likely and fluent output.  Apparently the baseline pattern matching methods used are really terrible:

1. EITHER: Up to the largest rule size/shape iterate over the (exponential in that size) many forest-topping label sequences, checking each against a rule label sequence hash.
2. OR: Iterate over all the rules, checking each one independently against the forest. 

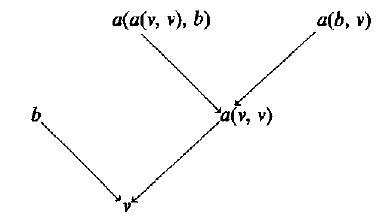
They give an improvement to the latter approach: if you’ve already matched the first 3 levels of a 4-height rule before, don’t repeat the work.  (The diagrams are pretty good; refer to them if you want to make sense of what follows). This is 20 times faster, and makes their overall MT system twice as fast.  If you’re actually using one of the above horrible baseline approaches, you would do well to emulate this paper.  I suspect that people are in practice using a hybrid of the two: exhaustively unpack the forest for a set of (small) top-of-tree-shapes e.g. x(x(x,x),x), retrieving potential rule sets by labels-hash, and then iterating over the resulting subset.  Unfortunately, they only compare their performance against the two (stupid) extremes.  I’ll also note that it always makes sense to (reversibly) binarize both the forest and the tree patterns in the same way, if you haven’t already, e.g. A(B,C,D) binarized would be: A(B,C_D(C,D)) where C_D is a virtual nonterminal that only appears in the context C_D(C(…),D(…)).

The avoidance of (some) repeated work is accomplished by 1) organizing tree patterns (rule left hand sides) to reflect these shared upper levels and 2) performing exhaustive top-down breadth-first expansion of pairs of (pattern state, forest states - one for each leaf in pattern state), where the forest states tuple may grow exponentially with depth.  Since we’re interested in the subforests aligned to the leaves of our tree pattern, we would take the forest states for pattern states corresponding to complete patterns, and perform some computation (MT in this case) on the subforests + pattern - we don’t just want the set of matching tree patterns.

This paper could have been clearer and shorter. The pseudocode has quirks.  It also seems to cite without reading: Decoding Complexity in Word-Replacement Translation Models (Knight 1999) does not show MT in general is NP-hard, only that IBM Model 1 (one of the simplest word to word translation models, with very free word reordering) is. MT based on parsing, without global features, is actually polynomial (albeit high degree if you have e.g. target 5gram probabilities).

Even though the forests arising from a parser will have the same root label for all trees in a state (e.g. NP covering words 1-2 has only NPs), I prefer the regular tree grammar formalism for a set of trees, where a grammar state can have production with different tree roots.  This paper handles the case where each state has a single unique tree root, since that’s what their parser gives them.  A general RTG production of rank k would need to be unpacked into N^k productions to achieve this, where N is the size of the tree label alphabet.  It’s better to modify your algorithm to use (root-label,forest-state) tuples instead of just (forest-state) whenever you want to look at only same-root trees.  I’m using “state” instead of the usual “nonterminal” to avoid confusion with the labels of the parse tree (in parsing, NP is a called a “nonterminal” of the tree NP(NN(dog))) since it’s not a “terminal”, or leaf).

Everything in the paper is called “hyper-X”.  There’s even a section called “hyper-node, hyper-path and hyper-tree”.  I appreciate the enthusiasm, but these are not great names, especially since they’re (misleadingly) suggestive of vertex/node, hyperpath, and hypertree in hypergraphs.  The forest is also given as a set of “hyper-edges” (without definition, but obviously they mean a directed B-hyperedges with ordered tails).

Obviously if the parse forest has probabilities attached to productions, you will have accumulated those in the process of finding a particular match.

The authors could have cited, for the related problem of matching a set of tree patterns against a single tree, Pattern Matching in Trees (Hoffman and O’Donnell 1982).  That work deals with ranked tree labels (doesn’t provide a way to say “subtree rooted in a NP of any arity”; you’d have to have NP(x) NP(x,x) NP(x,x,x) …), but that’s always a trivial change.  As far as I can tell, it’s impossible to use the top-down matching scheme in that paper efficiently on forests.

Hoffman and O’Donnell provide a helpful framework: the (immediate) subsumption graph of tree patterns.  This is a directed acyclic graph with edges from a to b if a>b (a>b (“subsumes”) iff \forall f a(f) => b(f)), where I’ve used a and b as predicates over trees or tree-sets f.  Immediate just means that only the necessary edges are kept (subsumption is transitive).  In the immediate subsumption graph pictured below, v means a variable, i.e. label can be anything:

Top-down matching procedures that report each assignment of subforests to tree pattern variables exactly once, will need to turn the subsumption graph into a tree.  Most likely you’ll want to do this in advance.  I’ve done this in a depth-first leftmost-expansion fashion by turning each tree pattern into a string, and combining the results into a trie with branching choice of “where to expand next”, implicitly giving a tree subgraph of the immediate subsumption graph (unpublished work).  Since I allow tree labels to have variable arity, I separate the choice of a label and its arity (the latter may never be specified).  My algorithm for matching this subsumption subgraph against a forest is the same as Zhang et. al, except that they’re breadth first, and they (unnecessarily) expand the whole level at once.  That is, their subsumption subgraph is not immediate.  They lose some sharing as a result, although it would be easy to fix this.  You can devise pattern sets that make a particular subsumption graph->tree mapping perform badly, and I don’t have any intuition as to whether theirs or mine will perform better on particular sets (e.g. MT rules containing most naturally occurring tree fragments up to a fixed size or depth).

The lost sharing from top-down matching any particular subsumption tree can be avoided entirely with bottom-up matching.  Hoffman+O’Donnell give a method for building a bottom-up deterministic tree recognizer, which is certainly optimal with respect to sharing and probably time if you can afford to precompute and store the (possibly exponential) monster.  Bottom up tree recognizers can match against forests beautifully, since regular tree grammars are closed under intersection.  Unlike top-down matching, the result of bottom-up matching would just be a set of rule (fragments) for each forest node.  To get the subforests, you’d have to traverse top-down (this should be pretty fast, since you’re constrained by a specific tree pattern).  In a future post, I’ll describe a bottom-up patterns against forest (or tree) matching that doesn’t explicitly determinize beforehand.  I’ll also note that the type of sharing you get in bottom up matching is avoiding work in repeatedly matching subtrees that are contained in different rules.  On the other hand, subsumption avoids repeated work in matching shared tops of trees.  That is, a pattern that subsumes another is always larger (turning some leaves into full subtrees).

Also, although I haven’t yet read it, A Simple Tree Pattern-Matching Algorithm claims to improve Hoffman+O’Donnell.  It’s unlikely that this would be useful for forest matching.